IsoPOPd: Theoretical Population Modeling for Understanding Growth Rates

The population matrix model

The population matrix model is a stage-structured demographic model that links vital rates in a life history to the population-scale dynamics that they generate (Tuljapurkar, 2008). Also known as the Leslie matrix (age structured; Leslie, 1945) or Lefkovitch (stage structured; Lefkovitch, 1965), the population matrix model has been used to enhance understanding of population viability of nearly 8,000 floral and faunal systems across the globe (see Salguero-Gomez et al., 2014, Salguero-Gomez et al., 2016).  The dominant eigenvalue of the model matrix is the single most important measure of population viability.  

The population matrix model has also been used in sensitivity analysis; that is, to understand the differential effects that targeted modifications to individual vital rates have on overall population dynamics (de Kroon et al., 2000). The capacity to reveal sensitivities between vital rates and growth rates makes the population matrix model a handy tool in identifying, exploring, and guiding the adoption of management alternatives in the pursuit of some management goal.

Taken together, these population viability and sensitivity analysis capabilities have made population matrix models the premier tool of population modeling.  

Vitals rates_IsoPOPd.png

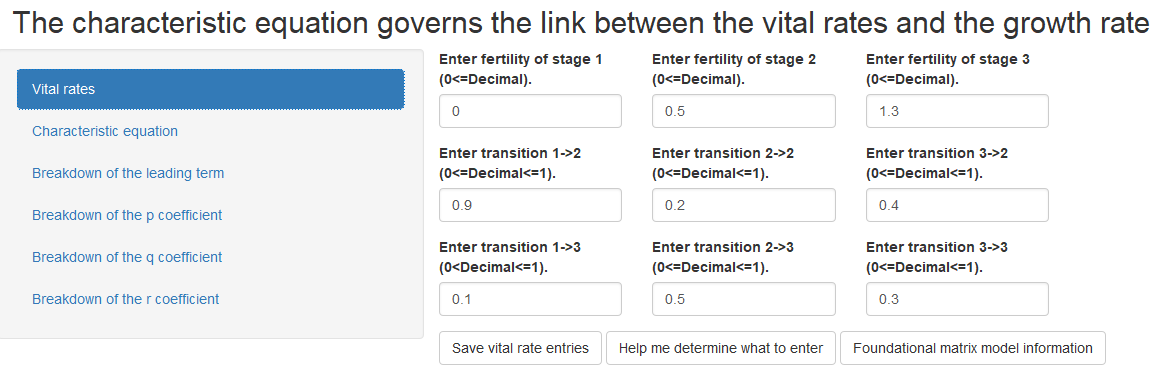
Instructions for use: 

Step 1: Input all nine vital rate magnitudes.  Vital rates must be positive real numbers.  Zero is a valid input for any given vital rate magnitude. 

Step 2: Save your entries.

Step 3: Navigate to the remaining tabs.

For each set of vital rate inputs, the code will produce a visualization of an eigenvalue cube, the visualization of the p volume, a visualization of the breakdown of the q volume and the visualization of the breakdown of the r volume.

The code will scale the dimensions of the volumes according to user inputs. 

IsoPOPd screen shot.png

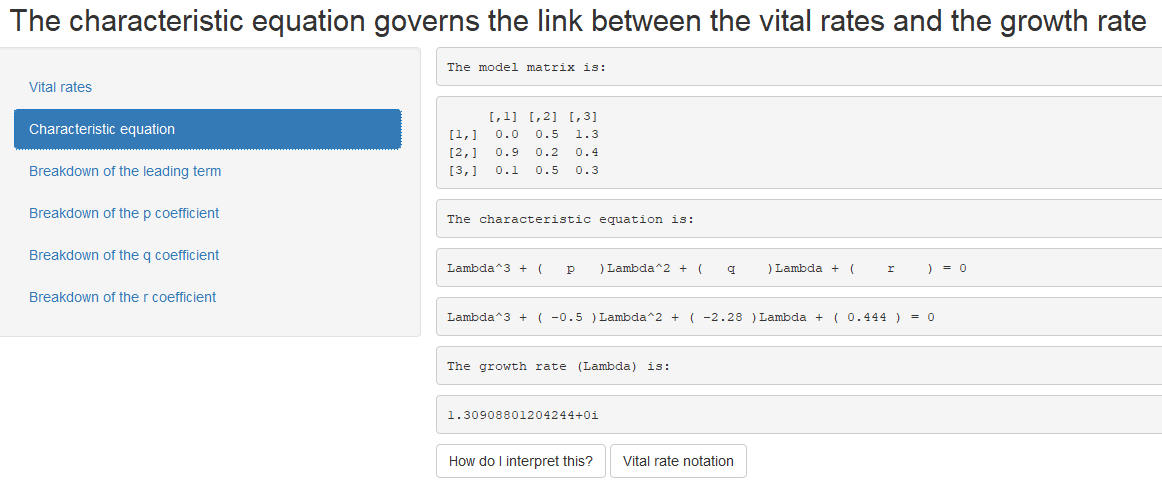
The software assumes a one-sex deterministic model matrix for an iteroparous species

These equations help us understand process at the expense of ecological detail, and therefore hinge on several simplifying assumptions.  The equations do not account for:

1) Carrying capacity,

2) Differential in life history traits that arise from genetic sources,

3) Differential in life history traits due to the sex ratio, 

4) Behaviour of the individuals over time, 

5) Any type of variation (demographic, environmental, sampling), 

6) Weather, climate, or seasonality, 

7) Competition with other species, 

8) Migration,

9) Predation. 

Although cause and effect may be altered by these real world ecological considerations, a tool to aid in understanding the deterministic processes are educational.  

• Do there appear to be any vital rates that have a stronger influence on the growth rate than others?    
• When you alter a life history characteristic, which superparameter does it change? (p, q, or r, or some combination of them?)
• Calculated volumes hinge on situational combination of vital rates. In the context of your system, what can be done if you wish to grow a population?  Shrink a population?  
• Are there any vital rates that functionally do not contribute to the growth rate?  
• Are there alterations that result in zero change to the growth rate?  
• Say you are a manager and you increase adult survival (alter a33).  Will a13 get more or less influential to the growth rate after the alteration?

IsoPOPd app in use.png

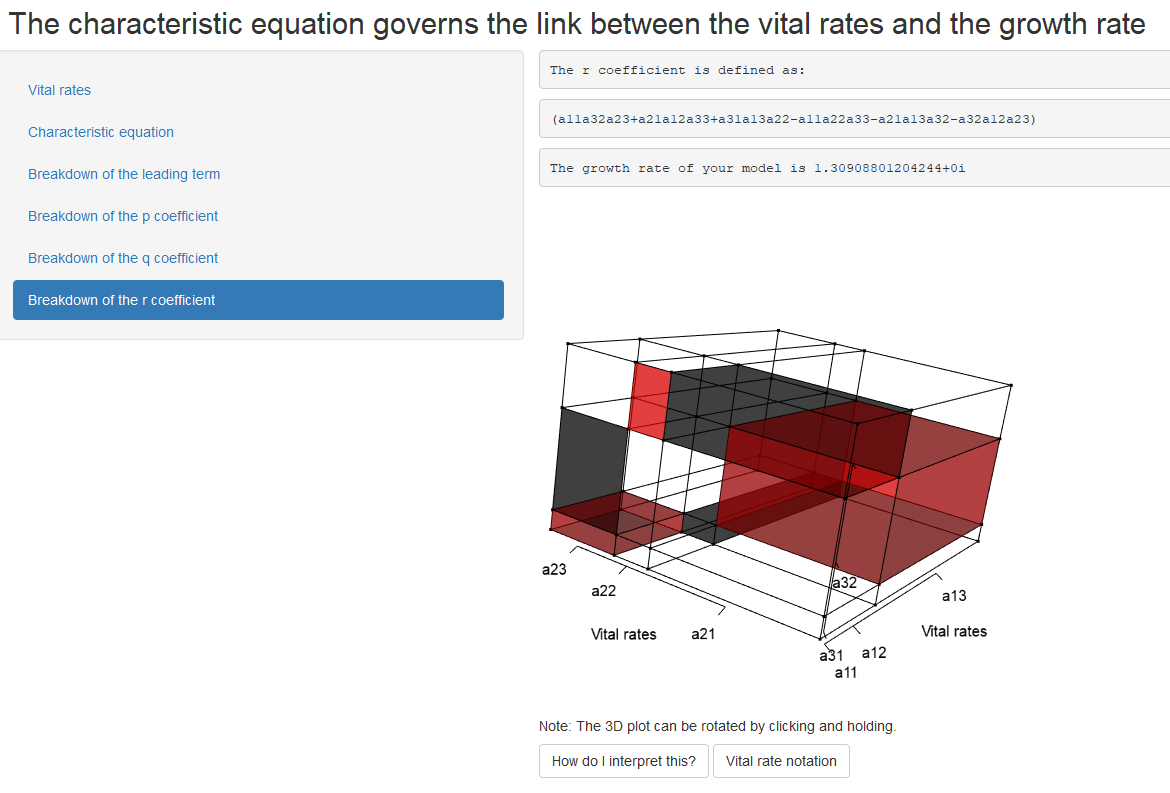
This software is described in:  

Hanley B, Connelly P, & Dennis B. 2019. Another look at the eigenvalues of a population matrix model. PeerJ 7:e8018. https://doi.org/10.7717/peerj.8018

Preferred citation for the use of this software:

Hanley B, Connelly P, & Dennis B. 2019. IsoPOPd: Interactive software to understand how elements in a population matrix model influence the asymptotic population growth rate [Software]. Cornell University Library eCommons Repository. doi: https://doi.org/10.7298/bcmg-7w08

The growth rate is calculated using long-established equations of population matrix models (Caswell, 2001).  Our contribution was to create these geometric illustrations of the balance equation, and make it accessible through an interactive app. 

Mathematical references

Caswell, H, (2001). Matrix population models: construction, analysis, and interpretation, 2 ed. Sinauer Associates, Inc, Sunderland, Massachusetts, USA.

de Kroon, H, van Groenendael, J, Ehrlén, J (2000). Elasticities: A review of methods and model limitations. Ecology, 81, 607–618.

Hanley, BJ, & Dennis, BC (2019). Analytical expressions for the eigenvalues, demographic quantities, and extinction criteria arising from a three-stage wildlife population matrix. Natural Resource Modelling.  

Lefkovitch, LP (1965).  The study of population growth in organism groups by stages.  Biometrics, 21, 1-18. 

Leslie, PH (1945).  On the use of matrices in certain population mathematics.  Biometrika, 33, 183-212.  

Tuljapurkar, S (2008). Stable population theory. The New Palgrave Dictionary of Economics. 2nd Edition. (eds). Steven N. Durlauf and Lawrence E. Blume. Palgrave Macmillan, United Kingdom.

Software references

R Core Team (2018). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria.  

R Shiny (2018). Shiny. Web Application Framework for R.  

RStudio Team (2015). RStudio: Integrated Development for R. RStudio, Inc., Boston, MA 

We’d also like to thank the R online user community (eg. several anonymous coders, Matthew Plourde) for providing example code and insight on programming around various obstacles (e.g. https://stackoverflow.com/questions/25455154/navlistpanel-make-tabs-sequ...).