"All models are wrong, but some are useful."
-George Box
You have likely heard this quote repeated during the COVID-19 pandemic. At quick glance, it seems to convey broad permission to comprehensively dismiss the use of models. But especially during this pandemic, when scientific models are crucial in identifying strategies that may be used to overcome our situation, I'd like to take a moment to more fully explain the first part of that quote, and highlight the importance of the second part. Let's start with the second part.
Models are useful.
In our world of mathematical ecology, a model is a mathematical representation of some ecological phenomena, and we use this representation to understand how that phenomena works.
In fact, models can teach us a tremendous amount about ecological systems, how we fit into it those systems, how we contribute to those systems, and - if things aren't going the way we want - what to do to try to influence them. These systems are naturally intricate, so the models that we build to represent them share that complexity. Accordingly, the lessons that we learn by analyzing them are not necessarily obvious.
When representing a natural process, the model will generally contain two broad parts: (1) a mathematical structure depicting that process and (2) some coefficients. The coefficients can take on many numerical values, and these values generally signify the importance of each portion of the equation, but the overall structure of the equation generally does not change. Given sufficient information on these two modeling components, you can leverage relationships among the variables to learn about processes that are unmeasurable or unobservable.
Let's dive into these modeling components using a simple demonstration. Let's say we went hiking up a mountain, and wanted to know the elevation of our lunch vista, but we had forgotten our GPS. We didn't have tool to measure the lunch elevation directly, so instead we looked around and took inventory of the tools that we had. We knew the elevation of the trailhead, the steepness of the trail, and had access to our wrist watch. We modeled the elevation using the equation for a line:
\(\Large Y = mX + b\)
Given this mathematical structure, if we were to start hiking from some starting elevation b, walk up the mountain of some fixed slope m for some duration X, then we will arrive at some lovely vista at elevation Y.
It doesn't matter if we are scaling a little foothill or climbing Mt. Everest, the general mathematical skeleton remains the same: the elevation where we enjoyed our lunch depended on where we started, how quickly we ascended, and the duration of our ascent.
What can change, however, are the values of the coefficients: the steepness of the slope (i.e. the value of m), the elevation of the trail head (i.e. the value of b), and maybe even the duration of our hike (i.e. the value of X). And unless our tools are perfect for the job, our ability to estimate the coefficients are constrained by the limitations of those tools and by our ability to operate those tools. So how does this estimation error (e) impact our lunch vista calculation? Well, in a lot of ways.
Imprecise coefficients impact our predictions. To see how, let's go back to our mountain example. Say, on our hike, that our watch battery died, so we were forced guess the duration of our walk (X). Well, any hiker knows that when left to our own devices, we get hungry and end up over-estimating lunch time (e.g. we think it is noon when its actually 10 a.m.). I suppose that one could also under-estimate lunch time, although that seems less plausible. In any event, we would have to account for that imprecision in our measurement.
Because we don't have a good idea of when we actually stopped for lunch, our minimum elevation at lunch could have been as low as:
\(\Large Y = m*X_{minimum} + b + e\)
while the maximum elevation could have been as high as:
\(\Large Y = m*X_{maximum} + b + e\)
Estimates of our final lunch elevation were therefore clouded by the fact that our lunch time was a guess.
The hiker's climb
Now let's say that our watch battery died and the slope of the mountain ended up being much more variable than we had anticipated. When we translate this scenario into numbers, we could have under- or over-estimated our slope m while simultaneously under- or over-estimating the duration of our hike, rendering the elevation of lunch as low as:
\(\Large Y = m_{minimum}*X_{minimum} + b + \varepsilon \)
or as high as:
\(\Large Y = m_{maximum}*X_{maximum} + b + \varepsilon \)
In the absence of precise coefficient values, our ultimate calculation of Y was indeed "off", which meant that the model - in the technical sense - was "wrong".
So yes, models can be "wrong".
In fact, any time we do not have the ability to accurately estimate each of the coefficients, subsequent model predictions will diverge from reality. Model predictions can also diverge from reality if the underlying mathematical skeleton diverges from reality. But the main reason why Box remarked that models were wrong was because models, by definition, are simplistic representations of complex natural mechanisms.
Despite being wrong, models are invaluable because the lessons that they provide are not limited to direct calculations. Using our hiking example, we could use our equation to (a) analyze the importance of the variables (e.g. determine whether it is more important to pack a spare watch or a spare slope measurement device), (b) fast-forward through time to see what the future might hold if conditions remain unchanged (e.g. determine whether it is worth holding off on lunch in order to get a better view), or (c) compare the underlying phenomena against something like it (e.g. compare coefficient values for several different mountains). As you can see, our simple hiking model could be used to learn about several aspects of our hike, and especially, how to better prepare our tools for the next one.
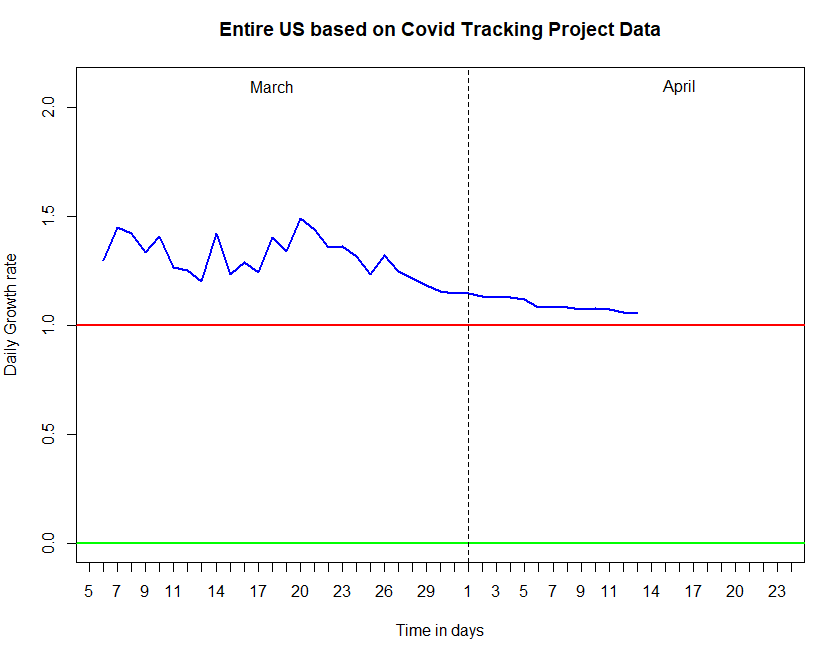
Graph from The COVID Tracking Project
Data taken at 4 p.m. for the entire US from March 4 – April 14 from The COVID Tracking Project
Models can reveal characteristics about phenomena that are illuminating, educational, and empowering. In fact, models are powerful tools because they teach us things about the phenomena that are not otherwise apparent.
In the case of COVID-19, the adaptation of fundamental epidemic equations with coefficient values that are specific to COVID-19 have produced models that are rapidly improving our understanding of the virus, how it works, and what we can do to slow its spread. We encourage you to take your newly found modeling perspective and explore an actual COVID-19 model!